지난번 글에서 공시의 부제 “인식 금액의 설명”에 관하여 나열하였다. 지루하고 어렵지만, 실제 어떤 형식으로 근거 측정 결과와 연결하여 측정결과의 정합성을 검증하고 기준서 위배 가능성을 정리하여 서술한 것인가에 관한 구체적 실무내용이라고 이해해 주기 바란다.이어서, 인식금액의 설명의 마지막 절 109에서 “(생략)기업은 보고기간 말에 언제 CSM을 이익으로 인식하는지 정량적(Quantitatively)으로 또한 정성적(Qualitatively) 적합한 배분 기간별로 공시하여야 한다. 이러한 정보는 원수계약과 보유 재보험계약 별도로 각각 제공하여야 한다.” 전편에서 강조하였듯이 RA도 계약의 경계를 넘어, 즉 미래 잔여 보험서비스 기간까지 만이 아니라 최종 종결 시점까지 보상 서비스 기간 종료 시점까지 배분하여야 한다.
공시 117-120까지 부제 “중대한 판단, IFRS17을 적용할 때”로 짧은 요건이 나열되어 있는데, 객관적으로 충족시키기가 쉽지 않다. 왜냐하면 판단의 근거를 정량적으로 제시하여야 하기 때문이다.
117. IFRS17을 적용함에 있어 중대한 판단 및 판단의 변경을 공시하여야 한다. 구체적으로 다음 사항을 포함하여 입력정보(Inputs), 가정 및 사용 추정기법을 공시하여야 한다.:
(a) IFRS17 적용범위 내의 보험계약을 측정하기 위하여 사용한 방법들과 그 방법들의 입력정보를 추정한 과정. 가능하다면, 그러한 입력정보에 대한 정량적 정보도 제공하여야 한다.
(b) 계약을 측정하기 위하여 사용한 방법과 입력정보 추정 과정의 모든 변경과 각 변경의 이유와 영향을 받은 계약의 유형
(c) (a)에서 다루지 않았다면 다음을 위해 사용한 방법:
(i) 재량의 행사에서 파생하는 미래 현금흐름 추정치의 변동과 직접 참가 특성이 없는 계약의 미래 현금흐름 추정치의 기타 변동을 구분하는(문단 B98 참조)
(ii) 비금융위험에 대한 위험조정 변동금액을 보험서비스요소와 보험금융요소로 세분하였는지 또는 전부 보험서비스 결과로 표시하였는지를 포함하여, 비금융위험에 대한 위험조정금액을 결정하는
(iii) 할인율 결정
(iv) 투자요소 결정
IFRS17을 적용함에 있어서 입력정보, 가정, 추정방법을 공시하여야 한다.(?) 너무도 어마어마한 내용이다. (a), (b), (c)를 포함한다. 점입가경이다. 더 나아가 (a)에서 보험계약의 측정방법과 그 측정방법의 입력변수(Input)를 추정하는 과정을 공시하여야 한다. Input에는 여러가지가 있다. 데이터, 가정(유지율, 손해액 진전계수(Loss development factor), 빈도, 심도 등등), 모수(Parameter; (로그)정규분포의 μ ?와 σ ?, Gamma 분포의 α ?와 β ?, 등), 추세율(Trend factor), 미래 추세(반영)기간 등 너무나도 많다. 물론 어떤 모델을 선택하느냐에 따라 Input은 다양하다. 많은 지식과 경험이 요구되는 계리적 실무내용이다. 학부에서 수학, 통계학 등을 전공하고 한국 계리사시험을 보는 것만으로는 너무도 불충분하다. 더구나, IFRS17에서 요구하는 측정방법론을 한번도 실무적으로 해본 경험이 없는 상태라면 더더욱 불가능하다. 충분히 이해는 하겠다. 그렇다고 비판을 안 할 수는 없다. 더 나아가, 예를 들어 (iii)할인율 혹은 무위험 수익율 곡선을 감독회계에 따라 금감원에서 제시한다는 것을 시장의 해외 자본들이 어떻게 이해할 것인가 생각해보자. 몇몇 회사가 별도로 할인율을 결정하여 적용하겠다고 하는 것은 별개의 이슈이다.
너무나 오랫동안 과거 보험감독원, 금융감독원이 정해주는 대로 하다 보니, 전문 지식 및 실무의 바탕인 보험 계리과학(Actuarial Science:?)의 토대와 뼈대, 그 위의 건물이 너무도 부실한 상황이다.
한가지 이와 관련하여 영국의 EMB사와 협업할 때 들었던 일화를 소개하겠다. 북미, 미국과 캐나다(물론 호주와 뉴질랜드로 같은 영연방이라 같을 것이다.)에서는 강제 가입보험(의무보험)을 제외한 임의 가입보험(임의보험)은 Pricing은 시장의 자율에 맡긴다. 자동차보험, 공적 보험인 산업재해보험(Workers’ Compensation)은 강제로 가입하여야 하므로 우리처럼 감독당국(각 주 단위의)의 승인을 받아야 한다. 그런데, 영국에 출장 갔을 때 일반화선형모델 소프트웨어인 EMBLEM 개발을 주도했던 파트너가 “EMBLEM이 영국 시장을 거의 장악하여 모든 회사가 자동차보험의 Ratemaking을 EMBLEM으로 하는데, 오직 한 회사만 알 수 없는 본인만의 방법 혹은 모델로 Ratemaking을 수행하고 있고 결과도 나쁘지 않다. 그런데, 그 회사의 대표 계리사가 본인 혼자서 보험료 수준을 정하고 다른 아무도 모른다.” 믿을 수가 없었다. 임의보험이 아닌 의무보험임에도 불구하고 영국은 시장에 자율로 보험료를 정하게 하고 있는 것이다. 20년도 더 지난 과거의 에피소드이다. Pricing, Ratemaking이 시장의 자율에 맡겨지는 것이다.
한편, 우리나라에서는 대학에서 학부, 대학원, 박사과정을 개설하여 운영할 주객관적 역량 또한 부재하다.
또 다른 에피소드를 소개하겠다. 필자가 6-7년전 캐나다에서 일하다 두번째로 한국에 돌아왔을 때, 업계 입문 7-8년된 직원이 “한국은 금감원이 정하는 바대로 무조건 해야 합니다.”라고 한적이 있다. 이미, 한국에서 유학 전 6년, 2002년 돌아와 2011년 캐나다로 돌아가기 전 10년 경력이 있는 사람에게 이런 말을 한다는 것은 실망을 넘어 얼마나 우물을 너머서 상황판단을 할 역량이 부족한지 가늠할 수 있다. 또 하나 소개할 에피소드는 생명보험 분야에서만 일을 해오던 직원이 “Triangle man”이라고 필자에게 부정적인 평가를 한적이 있다. 다차원 분석 및 모델링의 경험이 부재해서 생기는 일이다. 암담한 현실이다.
또한, 추정 기법, 측정 방법 혹은 모델을 방법론 차원에서 설명하는 것이 그다지 쉬운 것이 아니다. 추정(Estimation), 추정치(Estimate)는 통계학에서 익숙한 개념이다. 예를 들어 계리적 가정의 추정의 일부로서 Beta 분포의 모수(Parameter)인 α ?와 β ?를 추정하려면 최대우도함수(MLE: Maximum Likelihood Function)를 이용하여야 하는데, 간단히 구할 수 없고 소위 수치계산법(Numerical Method)을 이용하여야 한다. 그 방법도 여러가지이다. 수치계산법을 사용하기 위해서는 데이터가 필요한데, Sampling 기법을 사용하여 임의적(Random)으로 생성하여야 한다. 그 다음 모수를 이용하여 예컨대 유지율 분포를 확률론적으로 추정하려고 한다면 Monte-Carlo 방법을 선택하여 회차별 유지율 시나리오를 원하는 만큼 생성하수 있다. 물론 각 유지회차(월별, 분기별, 연별 등)별로 모델링하려면 추가적인 기술적 처리가 필요하다.
간단한 상품의 계약에 대해서는 현금흐름 추정치를 결정론적 방법을 이용하여 도출할 수 있지만, 기준서에 따르면 예외적인 경우로서 몇 개의 모수를 이용한 추정을 제시한다. 정규분포가 그 예일 것이다.
119. 비금융위험에 대한 위험조정 금액을 결정하기 위해 사용한 신뢰수준을 공시하여야 한다. 비금융위험에 대한 위험조정금액을 결정하기 위하여 신뢰수준기법 이외의 기법을 사용한다면 사용한 기법과 그러한 기법의 결과치에 해당하는 신뢰수준을 공시하여야 한다.
이에 관해서는 별도로 길게 다루겠지만, 본 고에서는 110절에 관한 원칙만 강조하고자 한다. 신뢰수준은 통계학에선 신뢰구간(Confidence Interval)과 관련한 개념이다. 여론조사와 관련하여 익숙하게 듣는 용어이기도 하다.
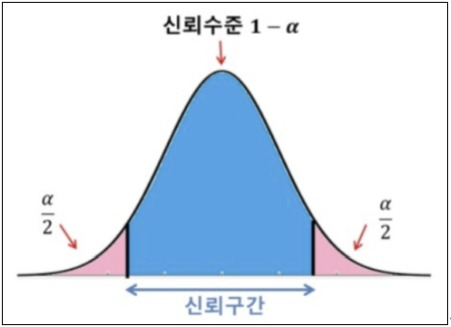
위 그래프에서, α를 0.1(10%)이라고 하면 신뢰구간의 파란영역은 분포의 90%에 해당된다. (+), (-)의 양측은 각각 0.05(5%)에 해당되며 표준정규분포의 경우 그에 따른 z값은 근사치 1.96을 구할 수 있다. 6σ 캠페인을 기억하는가? 99.999999999%, 즉 0.0000000001보다 작은 불량율, 오차율을 말하는 것이다.
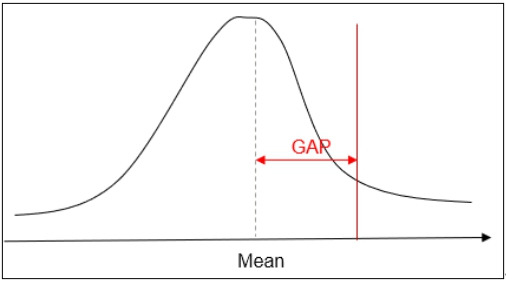
신뢰수준 기법은 VaR(Value at Risk)라고도 하며 위 그래프에서 보듯이 확률변수,즉 현금흐름의 분포를 추정하면 Mean 값과 기업에서 정한 신뢰수준, 예를 들어 75% 혹은 80% 등, 에 해당하는 확률변수 값과의 차이가 위험조정 값이 된다. 여기서, 또 한가지 지적할 점은 75%-tile이 누가 언제 어떻게 정했는가 하는 것이다. 그저 50%-tile인 중간값(Median)과 100%값의 중간 값이라고 편하게 말할 수 있지만 어떤 근거도 없다. 국제계리사회(IAA)에서 발간한 Monograph 위험조정(Risk Adjustment)을 보면 예제라고 하더라도 65%-tile, 90%-tile 등을 예시하고, 더 나아가 기업 특정(Entity specific)이기 때문에 사업부문, 포트폴리오 별로 신뢰수준이 다를 수도 있다고 설명하고 있다.
위 그래프는 CTE(Conditional Tail Expectation) 혹은 T-VaR(Tail VaR)라는 방법론이다. 신뢰수준을 정했다면 그 신뢰수준을 넘는 영역의 평균값을 택하는 것이다. 그 근거는 분포를 추정할 때 어느 데이터를 활용하였는 가와 만약 거대 손해액 청구 건이나 재해 사고 건을 반영하지 않았다면 VaR보다는 이 방법이 더 적합하다고 할 수 있다.
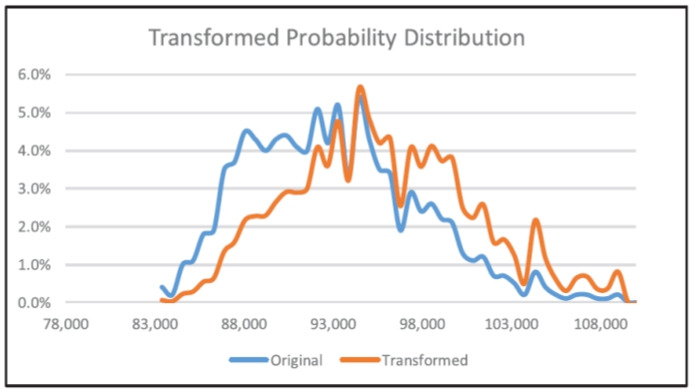
IAA Monograph, 위험조정에서 소개하는 왕변환(Wang Transform)도 참고하기 바란다. 상대적으로 큰 금액 영역의 예상 확률 크기를 확대하는 분포전환(Distribution transformation)의 한 예제 모델이다.
<svg version="1.1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" x="0" y="0" viewBox="0 0 27.4 20" class="svg-quote" xml:space="preserve" style="fill:#666; display:block; width:28px; height:20px; margin-bottom:10px"><path class="st0" d="M0,12.9C0,0.2,12.4,0,12.4,0C6.7,3.2,7.8,6.2,7.5,8.5c2.8,0.4,5,2.9,5,5.9c0,3.6-2.9,5.7-5.9,5.7 C3.2,20,0,17.4,0,12.9z M14.8,12.9C14.8,0.2,27.2,0,27.2,0c-5.7,3.2-4.6,6.2-4.8,8.5c2.8,0.4,5,2.9,5,5.9c0,3.6-2.9,5.7-5.9,5.7 C18,20,14.8,17.4,14.8,12.9z"></path></svg>
알려드립니다.
필자가 유튜브 방송 '유종환 TV'를 개설하였습니다. 일단 제소개를 우리말과 영어로 올렸으며, 2019년에 미래보험교육원에서 녹화했던 IFRS17 기준서 본문과 적용지침에 대한 해설 영상을 업로드하였습니다.
2020년 일부 수정된 부분은 추가적으로 동영상을 제작하여 올리겠지만, 지금 보니 기준서 본문 및 부록 적용지침 해설 총 35개 파일 20여 시간으로 방대해서 다 시청하기에 다소 힘들더라도 끈기를 가지고 이 기회에 “기준서 본문과 적용지침”을 한번 읽어 보다고 생각하고 동영상을 시청해 보시기를 권합니다.
한편, 더욱 방대하고 길어서, 그 당시에 자료는 준비되었지만 60여 시간 정도의 촬영시간이 예상되어 “결론의 근거”는 마저 촬영하지 못하였습니다. “결론의 근거” 또한 압축하여 핵심위주로 동영상을 신속히 만들어 업로드할 예정이니 기대해 주십시오.
이제 IFRS17 전면 시행시점이 두 달도 안 남은 시점에서 실무적 제3자 검증(Peer Review)이 더 긴급하다고 생각되어 우선 쉬운 계리적 모델 예제를 통하여 전고의 공시요건에 따른 검증과정 예제를 업로드하고자 합니다.
많은 관심과 시청 부탁드립니다.
유종환 법무법인 화현 금융전문위원 / 성균관대 보험계리학과 겸임교수 jong.yoo@jpartners.co.kr
