따라서 여러 개의 디지털 온도계가 모두 37.5℃를 가리키더라도 엄밀히 말해 다 같은 온도는 아니다. 따라서 측정 기계가 가진 한계를 넘어 보다 정밀한 값을 알고 싶다면 여러 번 측정해 얻은 값이나 여러 측정기가 동시에 측정한 값을 논리적으로 분석하는 과정이 필요하다. 사람의 눈으로 직접 관찰하는 경우에도 비슷한 문제가 있기는 매한가지다. 특정 종류의 새가 언제 알을 낳는지는 한 마리를 관찰했다고 자신있게 말할 수 있는 것이 아니다. 그렇다고 모든 새를 관찰하는 것도 현실적으로 불가능하다. 따라서 사람의 감각기관으로 직접 관찰하는 경우에도 여러 개의 관찰 결과로 전체 양상을 추정하는 과정이 필요하다.
이미 측정한 몇 개의 데이터로 아직 측정하지 않은 경우의 데이터를 예측하는 데는 확률이 사용된다. 대기권 밖의 단면적 A인 측정장치가 우주 먼 곳에서 폭발한 항성에서 방출된 입자 n개를 검출했다고 하자. 지구 반지름을 R이라고 할 때 지구의 전체 단면적 πR²에 동일한 확률로 입자가 도착할 것이라는 가정하에 지구 전체에 입사된 입자의 개수 N을 계산할 수 있다. 비례식에 의하면 n:N=A: πR²이므로 N=n(πR²/A)이다. 이같이 관찰하지 않은 값을 추정하기 위해 일정 범위 내에서 확률이 일정하다고 가정하는 것을 확률의 균등분포라고 한다. 확률의 균등분포를 사용하는 멋진 경우로 함수 그래프의 밑넓이를 추정하는 것이 있다. 오른쪽 [그림]은 한 변의 길이가 r인 정사각형 내부의 원 부분 밑넓이를 확률로 추정하기 위해 무작위로 점 8개를 찍어본 것이다.
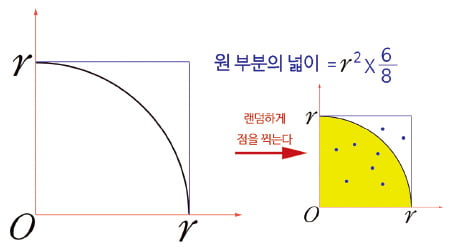
그림의 정사각형 내부에 동일한 확률로 위치를 바꾸며 점 8개를 찍었는데, 원 안에 들어간 점의 개수가 6개이므로 원 부분의 넓이 1/4πr²는 정사각형 넓이의 6/8 정도라고 추론할 수 있다. 이 결과로 원주율 π를 계산할 수도 있는데 π=4x(6/8)=3이다. 이런 방식으로 작동하는 프로그램을 실행해 점을 100만 개 찍으니 π=3.1404037이었다. 알려진 원주율의 값이 3.1415... 이므로 확률로 추정하는 결과는 측정 사례가 많아질수록 이론에 가까운 관찰 결과를 얻을 수 있음을 알 수 있다. 과학 기술 분야에서 그래프의 밑넓이를 계산하는 것을 적분이라 부른다. 수학적 논리만으로 적분 결과를 얻을 수 없을 때 확률의 균등분포를 이용하면 적분값을 추정할 수 있다. 이런 방법을 몬테카를로 방법이라 한다.
입자 가속기 내부에서 빠르게 가속된 입자를 하나의 목표점을 향해 충돌시키는 경우엔 충돌되는 면적 안에서 입자의 충돌 위치가 균등확률로 분포한다고 보기 어렵다. 마치 양궁 선수가 과녁을 향해 화살을 날리면 화살이 중앙점 가까이에 더 많이 모이는 것과 비슷하다. 이런 경우에 사용하는 확률 분포로 정규분포가 있다. 정규분포는 표준편차라고 부르는 수학 개념을 사용해 데이터가 평균 위치에서 벗어나는 경향을 반영할 수 있다. 따라서 양궁 선수가 과녁 중앙에서 벗어난 정도를 여러 개 반영한 표준편차를 계산해 해당 표준편차를 나타내는 정규분포를 살펴보면 과녁을 향해 쏜 화살이 몇 점 영역에 몇 개가 꽂힐지 예측할 수 있다. 이런 확률의 정규분포를 실생활에 이용하는 경우는 공장에서 생산된 제품을 임의로 추출해 전체 생산품의 품질을 추정하거나, 소수의 사람에게 질문해 전체 여론을 추론하는 일 등이 있다. 물리학이나 사회학의 실험 결과는 대부분 정규분포에 가까운 형태이므로 확률의 정규분포를 통계학의 꽃이라 부르는 사람도 있다. 직접 경험한 것을 통해 경험하지 않은 것을 정확하게 추론하려면 확률을 이용하면 된다.안종제 前 반포고 수석교사
