반면 온라인 게임에서부터 메타버스나 디지털트윈 등 다양한 이름을 갖는 디지털 공간에서 물체의 운동이나 변형을 현실감 있게 표현하려면 사람 사이의 언어가 아니라 수식으로 표현된 물리학적 개념이 컴퓨터 언어로 코딩돼야 합니다. 디지털 공간에서 현실 세계와 같은 다양하고 세밀한 물리적 현상을 표현할 수 있다면 외부에서 작용하는 힘에 대해 제품 또는 구조물의 운동이나 변형을 미리 예상해볼 수 있습니다. 관심 있는 환경 조건에서 물체의 운동이나 변형을 소프트웨어로 구체화해 놓고 검토하는 방법을 공학 분야에서는 CAE(computer-aided engineering)라고 합니다.
일반적으로 외력이 작용해 물체에 발생한 변형이 원래 형태로 회복 가능한지 여부나 변형이 점차 크거나 작아지는가에 따라 탄성(elasticity) 점탄성(viscoelasticity) 소성(plasticity) 개념을 활용할 수 있습니다.탄성은 단단한 스프링같이 외부에서 작용한 힘(외력)에 의해 조금이라도 즉각적으로 변화하면서 원래의 형태로 복원하려는 성질이라고 정의할 수 있는데, 물체가 변형하는 정도가 작용한 힘에 정비례하는 것으로 가정합니다. 튀어오르거나 복원되는 느낌을 나타내는 ‘탄성이 좋다’는 표현과 크게 다르지 않지만, 물리적 관점에서 조금 더 엄밀하게 정의하면 탄성이란 외력에 의해 변형이 즉각적으로 발생하면서 외력이 제거되면 즉각적으로 회복하는 조건을 만족해야 합니다. 적정한 외력이 작용하는 테니스공이나 쇠막대기, 시멘트 콘크리트가 대표적인 탄성재료로 분류됩니다.
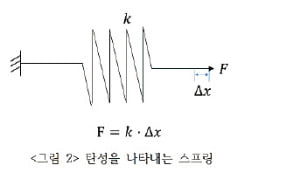
외력에 의해 형태가 즉각적으로 변하되 외력을 제거하더라도 원래대로 복원되지 않는 성질을 소성이라고 합니다. 모래에 새긴 발자국이나 밀가루 반죽에 남은 손가락 자국 등이 대표적인 소성 현상입니다. 생활에서 많이 사용되는 플라스틱 재질 소재는 뜨거운 온도에서 성형할 때 소성을 나타냅니다. 얼굴 형상을 변화시키는 성형 수술을 영어로 plastic surgery라고 하는 이유도 이런 특성을 반영했기 때문입니다.어떤 재료는 작은 힘에 대해 탄성을 나타내다가 큰 힘이 작용하면 소성을 보이는 탄소성(elastoplasticity) 특성을 지니기도 합니다. 이렇게 평소에 탄성에 가까운 특성을 나타내는 물체가 외력에 의해 소성을 나타내는 건 물체 내부에 균열이나 파손이 발생해 성질이 달라졌기 때문인 경우가 많은데, 물체의 성질이 달라지면 응력(힘, F)과 변형률(변위, △x)의 선형적 관계(응력=탄성계수×변형률)를 나타내는 탄성계수(스프링계수, k)가 변화할 뿐만 아니라 회복되지 않는 변형이 발생합니다. 반복적인 사용 또는 큰 외력에 의해 늘어나서 원래 형상으로 회복되지 않는 스프링이나 큰 힘으로 눌러서 일부 균열이 발생한 지우개가 대표적인 예라고 할 수 있습니다.
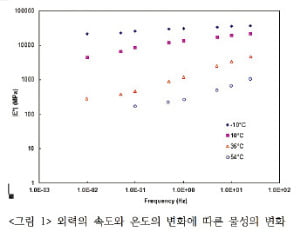
점탄성은 점성(viscosity)과 탄성을 결합한 성질입니다. 작용하는 외력의 시간적 특성에 따라 물체의 변형이 달라지는 특성을 표현하는 데 활용됩니다. 탄성과 소성으로 분류되는 소재로 만들어진 물체에 외력이 작용하면 작용하는 만큼 즉각적으로 변형이 발생하지만, 점탄성을 나타내는 물체는 힘이 일정하게 유지되더라도 변형이 점차 커지는 특성을 나타냅니다. 또한 점탄성을 지니는 물체는 동일한 크기의 외력이 작용하더라도 짧은 시간에 빠르게 작용시키면 변형이 적고 긴 시간 천천히 작용시키면 변형이 크게 발생하는 특성을 포함합니다. [그림 1]은 외력의 속도가 탄성계수에 어떻게 영향을 미치는지 점탄성으로 분류되는 소재에 대해 실험한 결과를 나타내고 있습니다. y축의 탄성계수는 x축의 외력 속도가 빨라질수록 증가하는 경향을 나타낼 뿐만 아니라, 범례에서 나타내는 네 가지 실험 온도에 대해서도 서로 다른 탄성계수를 보이는 것을 확인할 수 있습니다.
일반적인 산업에서 활용되는 탄성재료들은 영하 10도~영상 54도 범위에서 외력 속도에 따라 탄성계수가 거의 변하지 않는다는 점을 고려하면 매우 크게 변화한다는 것을 알 수 있습니다. 흔들리는 젤리나 형상을 천천히 복원하는 메모리폼 베게 등이 대표적인 점탄성 특성을 나타내는 물체입니다.
기억해주세요
탄성이나 점탄성, 소성은 힘에 따른 특정한 변형 특성을 나타내는 재료를 설명하기 위해 인간이 만들어낸 개념과 이론이기 때문에 자연계에 완전한 탄성, 점탄성, 소성 재료는 사실상 존재하지 않습니다. 또한 세상에는 이런 개념으로 충분히 설명할 수 있는 성질도 많이 있기 때문에 다양한 이론으로 설명돼야 합니다. 그러나 물체의 운동과 변형을 나타내기 위해 가장 처음 활용하는 개념이 [그림 2]에서 설명된 단순한 형태의 스프링입니다. 단순하기는 하지만 이미 우리는 디지털 공간을 표현하기 위한 기초를 고등학교 때부터 체계적으로 배우고 있습니다.